3秒でわかる「テイラー展開」

式
付近で近似するとして、
 をテイラー展開
をテイラー展開
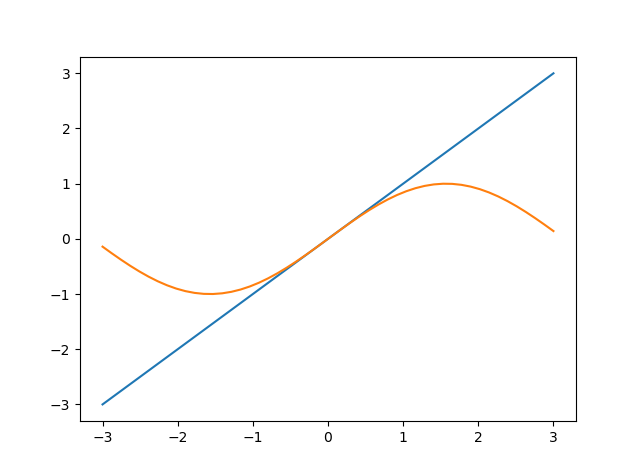
まずはx=0で1次近似します。
と
だとあまりにも違うので、次はx=0で2次近似をします。
なので、1次近似と同じ値になりました。次は3次近似をします。

少し近づきました!
計算していくとわかりますが、下記の式のようになります。

付近で近似するとして、
まずはx=0で1次近似します。
と
だとあまりにも違うので、次はx=0で2次近似をします。

なので、1次近似と同じ値になりました。次は3次近似をします。

少し近づきました!
計算していくとわかりますが、下記の式のようになります。